Skip to contents

Estimate Time-Varying Case Reproduction Number Using Wallinga-Lipsitch Method

Source: R/wallinga_lipsitch.R
wallinga_lipsitch.Rd

Estimates the time-varying case reproduction number (R_c) from daily incidence data using the method developed by Wallinga and Lipsitch (2007). The case reproduction number represents the average number of secondary infections generated by cases with symptom onset at time t, making it useful for retrospective outbreak analysis.

Usage

wallinga_lipsitch(
  incidence,
  dates,
  si_mean,
  si_sd,
  si_dist = "gamma",
  smoothing = 0,
  bootstrap = FALSE,
  n_bootstrap = 1000,
  conf_level = 0.95,
  shift = FALSE
)

Arguments

incidence

numeric vector; daily case counts. Must be non-negative integers or counts. Length must match dates

dates

vector; dates corresponding to each incidence count. Must be the same length as incidence. Can be Date objects or anything coercible to dates

si_mean

numeric; mean of the serial interval distribution in days. Must be positive. Typically estimated from contact tracing data or literature

si_sd

numeric; standard deviation of the serial interval distribution in days. Must be positive

si_dist

character; distribution family for the serial interval. Options:

  • "gamma" (default): Recommended for most applications as it naturally restricts to positive values

  • "normal": Allows negative serial intervals, useful when co-primary infections are suspected

smoothing

integer; window size for temporal smoothing of R estimates. Use 0 for no smoothing (default), or positive integers for moving average smoothing over the specified number of days

bootstrap

logical; whether to calculate bootstrap confidence intervals. Defaults to FALSE. Setting to TRUE increases computation time but provides uncertainty quantification

n_bootstrap

integer; number of bootstrap samples when bootstrap = TRUE. More samples provide more stable intervals but increase computation time. Defaults to 1000

conf_level

numeric; confidence level for bootstrap intervals, between 0 and 1. Defaults to 0.95 (95% confidence intervals)

shift

logical; whether to shift R estimates forward by one mean serial interval. When TRUE, adds a shifted_date column for comparison with instantaneous reproduction number estimates. Defaults to FALSE

Value

A data frame with the following columns:

  • date: Original input dates

  • incidence: Original input case counts

  • R: Estimated case reproduction number

  • R_corrected: Case reproduction number with right-truncation correction

  • R_lower, R_upper: Bootstrap confidence intervals for R (if bootstrap = TRUE)

  • R_corrected_lower, R_corrected_upper: Bootstrap confidence intervals for R_corrected (if bootstrap = TRUE)

  • shifted_date: Dates shifted forward by mean serial interval (if shift = TRUE)

Details

The method calculates the relative likelihood that each earlier case infected each later case based on their time differences and the serial interval distribution, then aggregates these likelihoods to estimate reproduction numbers. The approach makes minimal assumptions beyond specifying the serial interval distribution.

Key features:

  • Pairwise likelihood approach: Considers all epidemiologically plausible transmission pairs (earlier to later cases)

  • Right-truncation correction: Adjusts for unobserved future cases (see calculate_truncation_correction)

  • Bootstrap confidence intervals: Quantifies estimation uncertainty

  • Temporal shifting: Optional alignment with instantaneous R estimates

  • Flexible smoothing: User-controlled temporal smoothing of estimates

The Wallinga-Lipsitch method estimates the case reproduction number by:

  1. Computing transmission likelihoods from each earlier case to each later case based on the serial interval distribution

  2. Normalizing these likelihoods so they sum to 1 for each potential infectee

  3. Aggregating normalized likelihoods to estimate expected secondary cases per primary case

  4. Applying corrections for right-truncation bias

Right-truncation correction accounts for secondary cases that may occur after the observation period ends (see calculate_truncation_correction). This correction is particularly important for recent cases in the time series.

Bootstrap confidence intervals are calculated by resampling individual cases with replacement, providing non-parametric uncertainty estimates that account for both Poisson sampling variation and method uncertainty.

Note

The case reproduction number differs from the instantaneous reproduction number in timing: R_c reflects the reproductive potential of cases by their symptom onset date, while instantaneous R reflects transmission potential at the time of infection. Use shift = TRUE for comparisons with instantaneous R estimates.

References

Wallinga J, Lipsitch M (2007). How generation intervals shape the relationship between growth rates and reproductive numbers. Proceedings of the Royal Society B: Biological Sciences, 274(1609), 599-604. doi:10.1098/rspb.2006.3754

See also

si_estim for serial interval estimation, generate_synthetic_epidemic for testing data, calculate_truncation_correction for right-truncation correction

Examples

# Example 1: Basic usage with synthetic data
set.seed(123)
dates <- seq(as.Date("2023-01-01"), by = "day", length.out = 30)
incidence <- c(1, 2, 4, 7, 12, 15, 18, 20, 22, 19,
               16, 14, 11, 9, 7, 5, 4, 3, 2, 1,
               rep(0, 10))

# Estimate reproduction number
result <- wallinga_lipsitch(
  incidence = incidence,
  dates = dates,
  si_mean = 7,
  si_sd = 3,
  si_dist = "gamma"
)

# View results
head(result)
#>         date incidence         R R_corrected
#> 1 2023-01-01         1 18.651999          NA
#> 2 2023-01-02         2  9.587499    9.587576
#> 3 2023-01-03         4  5.705740    5.705825
#> 4 2023-01-04         7  3.529872    3.529970
#> 5 2023-01-05        12  2.253060    2.253175
#> 6 2023-01-06        15  1.466761    1.466898

# Example 2: With bootstrap confidence intervals
result_ci <- wallinga_lipsitch(
  incidence = incidence,
  dates = dates,
  si_mean = 7,
  si_sd = 3,
  si_dist = "gamma",
  bootstrap = TRUE,
  n_bootstrap = 500  # Reduced for faster example
)

# Plot results with confidence intervals
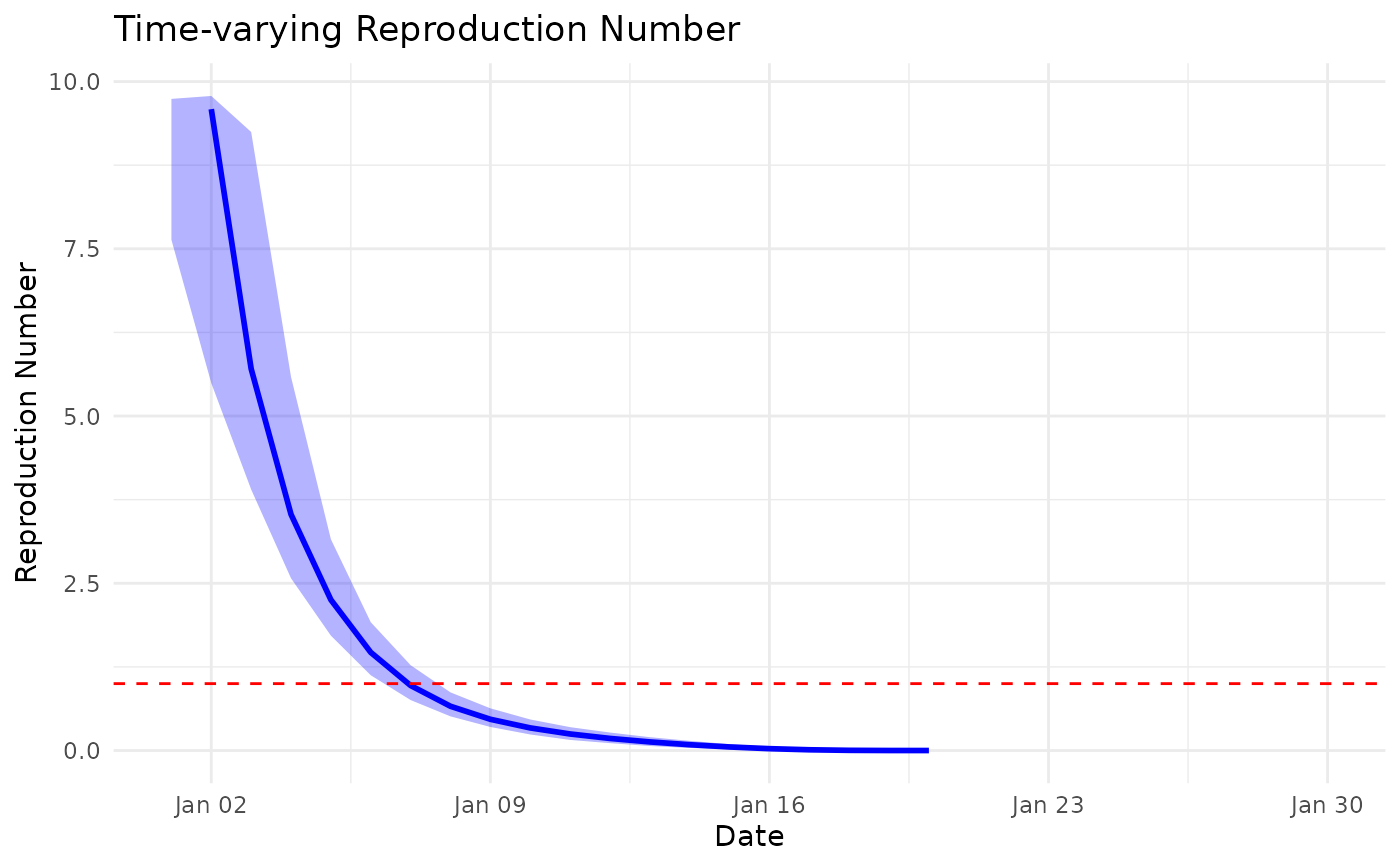
if (require(ggplot2)) {
  library(ggplot2)
  ggplot(result_ci, aes(x = date)) +
    geom_ribbon(aes(ymin = R_corrected_lower, ymax = R_corrected_upper),
                alpha = 0.3, fill = "blue") +
    geom_line(aes(y = R_corrected), color = "blue", size = 1) +
    geom_hline(yintercept = 1, linetype = "dashed", color = "red") +
    labs(x = "Date", y = "Reproduction Number",
         title = "Time-varying Reproduction Number") +
    theme_minimal()
}
#> Warning: Removed 10 rows containing missing values or values outside the scale range
#> (`geom_ribbon()`).
#> Warning: Removed 11 rows containing missing values or values outside the scale range
#> (`geom_line()`).


# Example 3: With smoothing and shifting
result_smooth <- wallinga_lipsitch(
  incidence = incidence,
  dates = dates,
  si_mean = 7,
  si_sd = 3,
  si_dist = "gamma",
  smoothing = 7,  # 7-day smoothing window
  shift = TRUE    # Shift for comparison with instantaneous R
)

# Example 4: Using normal distribution for serial interval
result_normal <- wallinga_lipsitch(
  incidence = incidence,
  dates = dates,
  si_mean = 6,
  si_sd = 2,
  si_dist = "normal",
  smoothing = 5
)